数据结构-二叉搜索树的前驱和后继节点
什么是二叉树的前驱节点和后继节点?
某节点的前驱节点的val值小于该节点的val值并且值是最大的那个节点。
某节点的后继节点的val值大于该节点的val值并且值是最小的那个节点。
下面给出一个二叉树节点类,和一个例子来说明。
package com.dzqc.yx.tree;
/**
* 节点类
* @author jiajia
* @param <T>
* @param <E>
*/
public class Node<T,E> {
/**
* 用于查找数据时比较的key
*/
public Integer key;
/**
* 数据
*/
public E e;
/**
* 父节点引用
*/
public Node<T,E> parent;
/**
* 左子节点引用
*/
public Node<T,E> left;
/**
* 右子节点引用
*/
public Node<T,E> right;
public Node(Integer key, E e) {
super();
this.key = key;
this.e = e;
}
public Node(Integer key, E e, Node<T, E> parent) {
super();
this.key = key;
this.e = e;
this.parent = parent;
}
public E setValue(E e) {
return this.e=e;
}
}
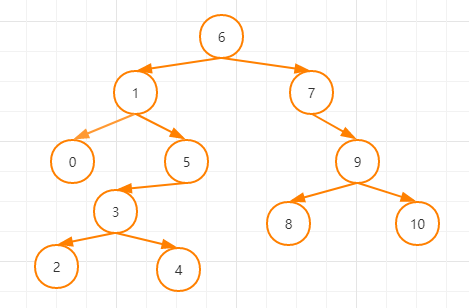
如上图:
1的前驱节点是0,4的前驱节点是3,6的前驱节点是5,3的前驱节点是2.
7的后继节点是8,9的后继节点是10,4的后继节点是5,2的后继节点是3
注意:上述的节点类都有对父节点的引用,如果没有父节点的引用将会用先序遍历的方式求,将会加大时间复杂度。
算法过程
某节点的前驱节点
- 若该节点有左子树,那么该节点的前驱节点是其左子树中val值最大的那个节点。
- 若该节点没有左子树,则判断该节点和其父节点的关系。
- 若该节点是其父节点的右子树,那么该节点的前驱结点就是其父节点。
- 若该节点是其父节点的左子树,那么沿着其父亲节点一直向树的顶端寻找,直到找到一个节点P,P节点是其父节点Q的右子树,那么节点Q就是该节点的后继节点。
某节点的后继节点
- 若该节点有右子树,那么该节点的后继节点是其右子树中val值最小的那个节点。
- 若该节点没有右子树,则判断该节点和其父节点的关系。
- 若该节点是其父节点的左子树,那么该节点的后继结点就是其父节点 。
- 若该节点是其父节点的右子树,那么沿着其父亲节点一直向树的顶端寻找,直到找到一个节点P,P节点是其父节点Q的左子树,那么节点Q就是该节点的后继节点。
java代码实现
前驱节点代码实现
/**
* 寻找前驱节点
* @param t
* @return
*/
public Node<Integer,Integer> precursor(Node<Integer,Integer> t){
if(t!=null) {
if(t.left!=null) {
Node<Integer,Integer> p=t.left;
while(p.right!=null)
p=p.right;
return p;
}else {
if(t==t.parent.right) {
return t.parent;
}else {
Node<Integer,Integer> p=t.parent;
while(p!=null&&p!=p.parent.right) {
p=p.parent;
}
return p.parent;
}
}
}else {
return null;
}
}
前驱节点测试
/**
* 前驱节点
*/
@Test
public void test24() {
Node<Integer,Integer> n6=new Node<>(6,6,null);
Node<Integer,Integer> n1=new Node<>(1,1,n6);
Node<Integer,Integer> n5=new Node<>(5,5,n1);
Node<Integer,Integer> n3=new Node<>(3,3,n5);
Node<Integer,Integer> n2=new Node<>(2,2,n3);
Node<Integer,Integer> n4=new Node<>(4,4,n3);
Node<Integer,Integer> n7=new Node<>(7,7,n6);
Node<Integer,Integer> n9=new Node<>(9,9,n7);
Node<Integer,Integer> n8=new Node<>(8,8,n9);
Node<Integer,Integer> n10=new Node<>(10,10,n9);
n6.left=n1;
n6.right=n7;
n1.right=n5;
n5.left=n3;
n3.left=n2;
n3.right=n4;
n7.right=n9;
n9.left=n8;
n9.right=n10;
System.out.println(precursor(n10).key);
}
后继节点代码实现
/**
* 寻找后继节点
* @param t
* @return
*/
public Node<Integer,Integer> successor(Node<Integer,Integer> t) {
if (t == null)
return null;
else if (t.right != null) {
Node<Integer,Integer> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
Node<Integer,Integer> p = t.parent;
Node<Integer,Integer> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
后继节点测试
/**
* 后继节点
*/
@Test
public void test23() {
Node<Integer,Integer> n6=new Node<>(6,6,null);
Node<Integer,Integer> n1=new Node<>(1,1,n6);
Node<Integer,Integer> n5=new Node<>(5,5,n1);
Node<Integer,Integer> n3=new Node<>(3,3,n5);
Node<Integer,Integer> n2=new Node<>(2,2,n3);
Node<Integer,Integer> n4=new Node<>(4,4,n3);
Node<Integer,Integer> n7=new Node<>(7,7,n6);
Node<Integer,Integer> n9=new Node<>(9,9,n7);
Node<Integer,Integer> n8=new Node<>(8,8,n9);
Node<Integer,Integer> n10=new Node<>(10,10,n9);
n6.left=n1;
n6.right=n7;
n1.right=n5;
n5.left=n3;
n3.left=n2;
n3.right=n4;
n7.right=n9;
n9.left=n8;
n9.right=n10;
System.out.println(successor(n10));
}
fixed
没有一个冬天不可逾越,没有一个春天不会来临。最慢的步伐不是跬步,而是徘徊,最快的脚步不是冲刺,而是坚持。
