什么是floyd算法

在计算机科学中，Floyd-Warshall算法是一种在具有正或负边缘权重（但没有负周期）的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度（加权）。 虽然它不返回路径本身的细节，但是可以通过对算法的简单修改来重建路径。 该算法的版本也可用于查找关系R的传递闭包，或（与Schulze投票系统相关）在加权图中所有顶点对之间的最宽路径。

案例

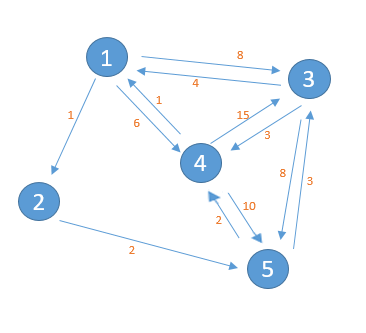如有一个图（可以理解为一个地图），图中有5个顶点，顶点A到顶点B之间有连线代表从点A可以直接到点B，该线段的权值可以理解为两点间的距离。那么从下边的图中可以了解到从顶点1到顶点2的距离为1，顶点2到顶点5的距离为2…但是从顶点2无法到达顶点4，但是可以通过顶点5中转到达。

该图表示一个有向图，例如从顶点1可以到达顶点2，他的权值为1，但是从顶点2无法直接到达顶点1。

两顶点之间箭头的值代表该路径的权值，即顶点1到顶点2的消费。

 

问题

比如从1直接到4的距离为6，但是从点1，经过2，在经过5到达点4的距离为2。显然中转的方式，比直接到达的方式更好。

所以为了方便解决问题，把图的信息用一个二维数组r来描述。 （采用图的邻接矩阵表示）

顶点	1	2	3	4	5
1	0	1	8	6	∞
2	∞	0	∞	∞	2
3	4	∞	0	3	8
4	1	∞	15	0	10
5	∞	∞	3	2	0

其中r[i][j]=n表示从顶点i到顶点j的距离为n。

方案

例如顶点4到顶点3，直接到达的距离为15，而通过顶点5中转距离就会缩短为5。

开始时，各顶点之间的原始距离为：（∞表示正无穷，可以理解为一个很大很大的数）

顶点	1	2	3	4	5
1	0	1	8	6	∞
2	∞	0	∞	∞	2
3	4	∞	0	3	8
4	1	∞	15	0	10
5	∞	∞	3	2	0

如果只通过顶点1中转，那么如何计算任意两点之间的最短路呢？答案是只需要判断r[i][1]+[1][j]和r[i][j]的大小即可。如果r[i][1]+[1][j]比r[i][j]小，那么就表示通过顶点1中转时的路径要比直接到达短。

比如从顶点4到顶点2即r[4][2]=∞（无法到达）,但是通过顶点1中转以后路径变为r[4][1]+r[1][2]=2,显然比r[4][2]要小。

顶点	1	2	3	4	5
1	0	1	8	6	∞
2	∞	0	∞	∞	2
3	4	5	0	3	8
4	1	2	9	0	10
5	∞	∞	3	2	0

对应代码如下：

for(int i=0;i<r.length;i++) {
	for(int j=0;j<r.length;j++) {
		if(r[i][j]>r[i][0]+r[0][j]) {
			r[i][j]=r[i][0]+r[0][j];
		}
	}
}

可以发现，经过顶点1时，从顶点3到2，顶点4到2，顶点4到3的距离都变短了。

顶点	1	2	3	4	5
1	0	1	8	6	3
2	∞	0	∞	∞	2
3	4	5	0	3	7
4	1	2	9	0	10
5	∞	∞	3	2	0

 代码如下：

for(int i=0;i<r.length;i++) {
	for(int j=0;j<r.length;j++) {
		if(r[i][j]>r[i][0]+r[0][j]) {
			r[i][j]=r[i][0]+r[0][j];
		}
	}
}
for(int i=0;i<r.length;i++) {
	for(int j=0;j<r.length;j++) {
		if(r[i][j]>r[i][1]+r[1][j]) {
			r[i][j]=r[i][1]+r[1][j];
		}
	}
}

可以发现，经过顶点1和2时，从顶点1到5，顶点3到5的距离又变短了。

一次类推

......

...

.

顶点	1	2	3	4	5
1	0	1	6	5	3
2	5	0	5	4	2
3	4	5	0	3	7
4	1	2	7	0	4
5	3	4	3	2	0

 对应代码如下：

for(int k=0;k<r.length;k++) {
	for(int i=0;i<r.length;i++) {
		for(int j=0;j<r.length;j++) {
			if(r[i][j]>r[i][k]+r[k][j]) {
				r[i][j]=r[i][k]+r[k][j];
			}
		}
	}
}

当中转完成所有的顶点的时候，那么数组中就是最终的结果。

对于上面的几行代码就是Floyd算法的核心。

对于正无穷怎么表示，可以根据具体的情况设置一个较大的值表示。

Floyd-Warshall算法是动态规划的一个例子,该算法也称为Floyd算法，Roy-Warshall算法，Roy-Floyd算法或WFI算法。

它的状态转移方程就是：r[i][j]=min(r[i][j],(r[i][k]+r[k][j]))

另外需要注意的是：Floyd-Warshall算法不能解决带有“负权回路”（或者叫“负权环”）的图，因为带有“负权回路”的图没有最短路。

优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。

缺点：时间复杂度比较高o(n³)，不适合计算大量数据。

 

完整测试代码

import org.junit.Test;

/**
 * floyd
 * @author jiajia
 *
 */
public class TestMain {
	/**
	 * a用来表示正无穷
	 */
	public static final int a=Integer.MAX_VALUE>>3;
	/**
	 * r表示图的顶点和边的关系
	 */
	public static final int r[][]=new int[][] {
		{0,1,8,6,a},
		{a,0,a,a,2},
		{4,a,0,3,8},
		{1,a,15,0,10},
		{a,a,3,2,0}
	};
	/**
	 * 算法核心
	 */
	public static void floyd() {
		for(int k=0;k<r.length;k++) {
			for(int i=0;i<r.length;i++) {
				for(int j=0;j<r.length;j++) {
					if(r[i][j]>r[i][k]+r[k][j]) {
						r[i][j]=r[i][k]+r[k][j];
					}
				}
			}
		}
		for(int i=0;i<r.length;i++) {
			for(int j=0;j<r.length;j++) {
				System.out.print(r[i][j]+"\t");
			}
			System.out.println();
		}
	}
	
	/**
	 * 只经过顶点1
	 */
	@Test
	public void r1() {
		for(int i=0;i<r.length;i++) {
			for(int j=0;j<r.length;j++) {
				if(r[i][j]>r[i][0]+r[0][j]) {
					r[i][j]=r[i][0]+r[0][j];
				}
			}
		}
		for(int i=0;i<r.length;i++) {
			for(int j=0;j<r.length;j++) {
				System.out.print(r[i][j]+"\t\t\t");
			}
			System.out.println();
		}
	}
	
	/**
	 * 只经过顶点1和点2
	 */
	@Test
	public void r2() {
		for(int i=0;i<r.length;i++) {
			for(int j=0;j<r.length;j++) {
				if(r[i][j]>r[i][0]+r[0][j]) {
					r[i][j]=r[i][0]+r[0][j];
				}
			}
		}
		for(int i=0;i<r.length;i++) {
			for(int j=0;j<r.length;j++) {
				if(r[i][j]>r[i][1]+r[1][j]) {
					r[i][j]=r[i][1]+r[1][j];
				}
			}
		}
		for(int i=0;i<r.length;i++) {
			for(int j=0;j<r.length;j++) {
				System.out.print(r[i][j]+"\t\t\t");
			}
			System.out.println();
		}
	}
	/**
	 * @param i
	 * @param j
	 * @return
	 */
	public static int r(int i,int j) {
		return r[i-1][j-1];
	}
	/**
	 * @param args
	 */
	public static void main(String[] args) {
		floyd();
		System.out.println(r(1,2));
	}
}