leetcode第62题（中等）【动态规划 dp】

原链接：https://leetcode-cn.com/problems/unique-paths/

题目描述

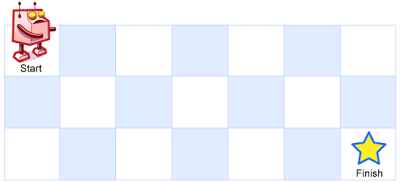
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例1

输入：m = 3, n = 7
输出：28

示例2

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

解题思路

动态规划，状态转移方程：

两种方案：

1.从开始节点到目标节点推算：dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

2.从目标节点到开始节点推算：dp[i][j]=dp[i+1][j]+dp[i][j+1];

代码

一般解法

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp=new int[n][m];
        for(int i=n-1;i>=0;i--){
            for(int j=m-1;j>=0;j--){
                if(i==n-1||j==m-1){
                    dp[i][j]=1;
                }else{
                    dp[i][j]=dp[i+1][j]+dp[i][j+1];
                }
            }
        }
        return dp[0][0];
    }
}

优化一下空间复杂度（状态压缩）

class Solution {
    public int uniquePaths(int m, int n) {
        int[] mm=new int[m];
        int[] nn=new int[n];
        for(int i=n-1;i>=0;i--){
            for(int j=m-1;j>=0;j--){
                if(i==n-1||j==m-1){
                    mm[j]=nn[i]=1;
                }else{
                    mm[j]=nn[i]=mm[j]+nn[i];
                }
            }
        }
        return mm[0];
    }
}