leetcode第48题（中等）

原链接：https://leetcode-cn.com/problems/rotate-image/

问题描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例1

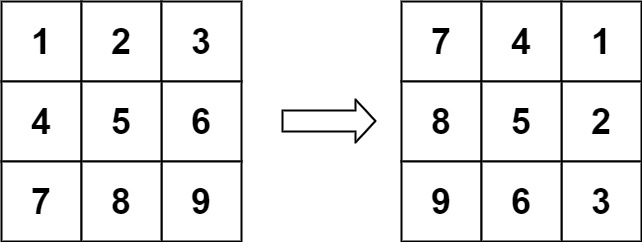
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例2

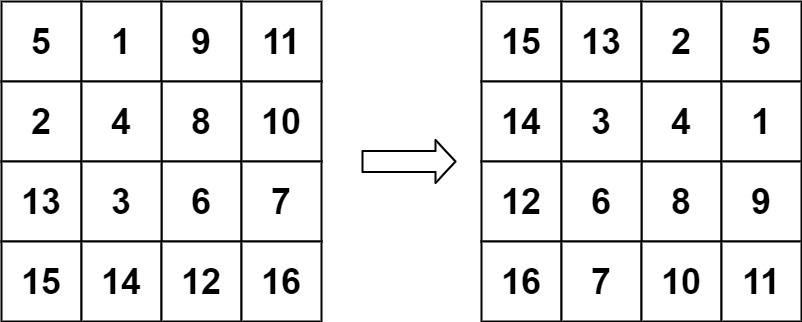
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

解法1（我比较容易想到的）

顺时针旋转后的数组，其实就是原数组从左下角开始从下到上，从左到右遍历的结果。第一种解法要用到一个临时数组拷贝原数组，然后从左下角开始从下到上，从左到右遍历临时数组，将值赋给原数组。显然这种方式，要消耗更多的空间。

代码

class Solution {
    public void rotate(int[][] matrix) {
            int l=matrix.length;
            int [][] a=new int[l][];
            for(int i=0;i<l;i++){
                a[i]=matrix[i].clone();
            }
            for(int i=0;i<l;i++){
                for(int j=l-1;j>=0;j--){
                    matrix[i][l-j-1]=a[j][i];
                }
            }
        }
}

解法2（别人能想到的）

这种方法是按层遍历，从内到外遍历每一层，将某层的各个位置的数据都赋值完成，在遍历下一层。这种方案不需要临时数组，直接可以在原数组上操作。

代码

class Solution {
public void rotate(int[][] matrix) {
        int s = 0, n = matrix.length;
        while (s < (n >> 1)) {
            int e = n - s - 1;
            for (int i = s; i < e; ++i) {
                int t = matrix[i][e];
                matrix[i][e] = matrix[s][i];
                matrix[s][i] = matrix[n - i - 1][s];
                matrix[n - i - 1][s] = matrix[e][n - i - 1];
                matrix[e][n - i - 1] = t;
            }
            ++s;
        }
    }
}