优先级队列
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征。通常采用堆数据结构来实现。
优先级队列 是不同于先进先出队列的另一种队列。每次从队列中取出的是具有最高优先权的元素。
操作:
1.往队列中添加数据
2.从队列中获取数据
优先级队列通常采用堆数据结构处理
用数组实现
文档下载: java数组实现优先级队列(小顶堆).docx
java数组实现优先级队列(小顶堆).docx
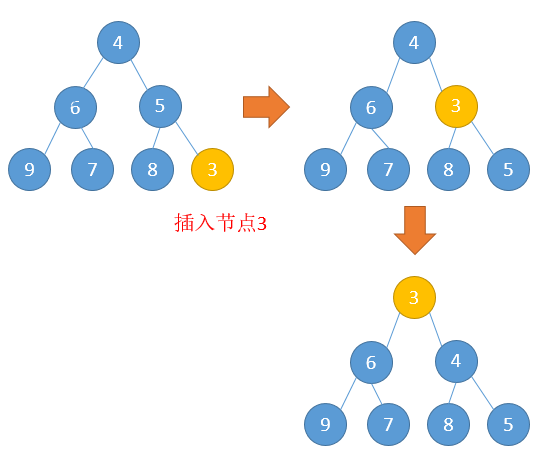
插入数据:
算法:
先将数据插入到数组末尾,然后进行上浮操作,
如果父节点大于大于该子节点,则执行上浮操作,直到该节点为根节点。
//交换
private void exchange(int i,int j) {
queue[i]=queue[i]+queue[j];
queue[j]=queue[i]-queue[j];
queue[i]=queue[i]-queue[j];
}
//上浮
private void swim(int k) {
while (k > 1 && compare(k>>1, k)) {
exchange(k, k>>1);
k = k>>1;
}
}
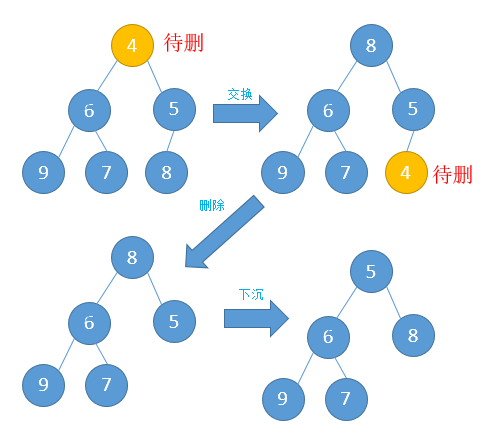
从队列中获取数据
算法:
把数组首节点和尾节点交换,删除尾节点,队列元素个数-1,此时队列可能不满足优先队列的条件,需要执行下沉操作。
具体是先比较下沉节点的的两个子节点的元素大小,选择较小的子节点交换,反复进行此操作,直到树的叶子节点。
private void sink(int k) {
while (k<<1 <= n) {
int j = k<<1;
if (j < n && compare(j, j+1))
j++;
if (!compare(k, j))
break;
exchange(k, j);
k = j;
}
}
代码实现:
package com.itdragon.controller;
/**
* 优先级队列(小顶堆)
* @author JIA_JIAJIA
* @website http://www.jiajiajia.club
* @da2019年5月11日
*/
public class PriorityQueue {
/**
* 队列元素
*/
private int queue[];
/**
* 队列长度
*/
int n;
/**
* 循序打印数组中的值,相当于二叉树的层级遍历
*/
public void printf() {
for(int i=1;i<n+1;i++) {
System.out.print(queue[i]+" ");
}
}
/**
* 初始化队列大小
* @param size
*/
public PriorityQueue(int size) {
/**
* 初始化队列的元素数组,和队列大小
*/
queue=new int[size+1];
n=0;
}
/**
* 插入数据到队列中
* @param data
* @return
*/
public boolean insert(int data) {
/**
* 如果数组容量不够则进行扩容操作(在原来数组容量的基础上+10)
*/
if (n >= queue.length - 1)
queue=java.util.Arrays.copyOf(queue,queue.length+10);
queue[++n] = data;
swim(n);
System.out.println(isPriorityQueue());
return true;
}
/***
* 从队列中获取数据
* @return
*/
public int getDate() {
int data = queue[1];
exchange(1, n);
n--;
sink(1);
queue[n+1]=0;
if ((n > 0) && (n == (queue.length - 1) / 4))
queue=java.util.Arrays.copyOf(queue,queue.length/2);
System.out.println(isPriorityQueue());
return data;
}
/**
* 比较元素的大小,queue[i]>queue[j]返回true,queue[i]<queue[j]返回false
* @param i
* @param j
* @return
*/
public boolean compare(int i,int j) {
return queue[i]>queue[j]?true:false;
}
/**
* 交换queue中i位置和j位置的值
* @param i
* @param j
*/
private void exchange(int i,int j) {
/**
* 不用第三个变量做中间变量,交换两个整数变量的值
* 例:
* a=a+b;
* b=a-b;
* a=a-b;
* 这样a,b的值就交换了
*/
queue[i]=queue[i]+queue[j];
queue[j]=queue[i]-queue[j];
queue[i]=queue[i]-queue[j];
}
/**
* 上浮操作
* @param k 数组下标k
*/
private void swim(int k) {
/**
* 对于小顶堆,如果父节点的值大于该子节点,那么交换该节点和父节点,然后继续比较该节点与父节点...
* 直到该节点是根节点。
* 右移(>>)相当于除以2,参考 http://www.jiajiajia.club/blog/artical/200
*
* 用数组表示二叉树,有如下性质
* 子节点的下标位置>>2等于父节点的下标位置。适用于左节点和右节点。
*/
while (k > 1 && compare(k>>1, k)) {
exchange(k, k>>1);
k = k>>1;
}
}
/**
* 下沉操作
* @param k 数组下标k
*/
private void sink(int k) {
/**
* 从头结点开始,如果当前节点还有子节点,则一直判断是否还可以下沉
*/
while (k<<1 <= n) {
int j = k<<1;//
/**
* j当前节点的左节点,compare(j, j+1)是为了比较做节点大,还是右节点大
* 从而可以判断父节点是向左节点下沉,还是右节点下沉,如果是向右节点下沉则j++
*/
if (j < n && compare(j, j+1))
j++;
/**
* 如果父节点小于子节点的最小值,则下沉结束。
*/
if (!compare(k, j))
break;
/**
* 交换子节点和父节点,当前节点变为子节点,继续判断是否还可以下沉
*/
exchange(k, j);
k = j;
}
}
/**
* 判断是否满足堆得性质
* @return
*/
private boolean isPriorityQueue() {
return isPriorityQueue(1);
}
/**
* 递归遍历判断该堆是否满足堆得性质
* @param k
* @return
*/
private boolean isPriorityQueue(int k) {
if (k > n)
return true;
/**
* 左子树下标位置
*/
int left = k<<1;
/**
* 右子树下标位置
*/
int right = k<<1 + 1;
if (left <= n && compare(k, left))
return false;
if (right <= n && compare(k, right))
return false;
/**
* 递归遍历左右子树
*/
return isPriorityQueue(left) && isPriorityQueue(right);
}
}
package com.itdragon.controller;
import org.junit.Test;
/**
* @author JIA_JIAJIA
* @website http://www.jiajiajia.club
* @da2019年5月11日
*/
public class TestMain2 {
@Test
public void test() {
PriorityQueue pq=new PriorityQueue(10);
pq.insert(9);
pq.insert(8);
pq.insert(7);
pq.insert(6);
pq.insert(5);
pq.insert(4);
System.out.println(pq.getDate());
pq.printf();
}
}



