在关于树的多种算法中都用到了树的旋转来使树保持相对平衡,比如avl树,红黑树等...
1.树的左旋(pivot为旋转中心点)
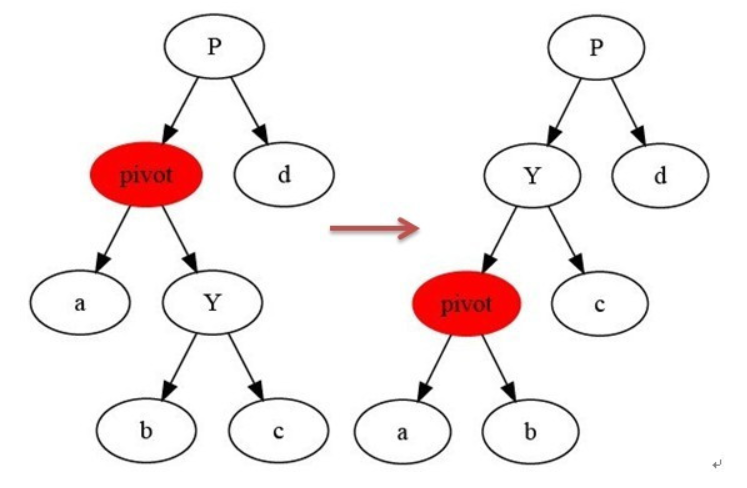
2.来个动图
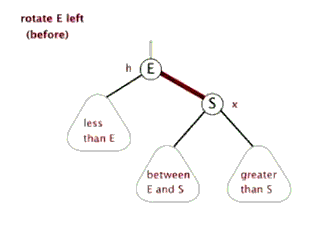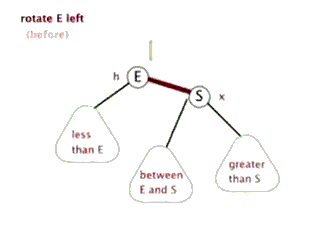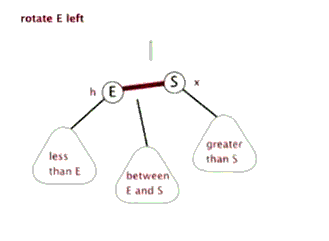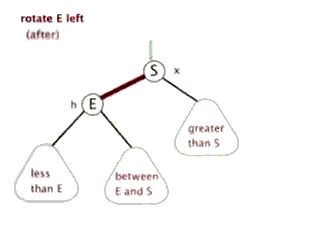
3.代码演示:
/**
* 左旋
* p为旋转的中心点
*/
public void rotateLeft(Node<T,E> p) {
if (p != null) {
Node<T,E> r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
4.树的右旋(pivot为旋转中心点)
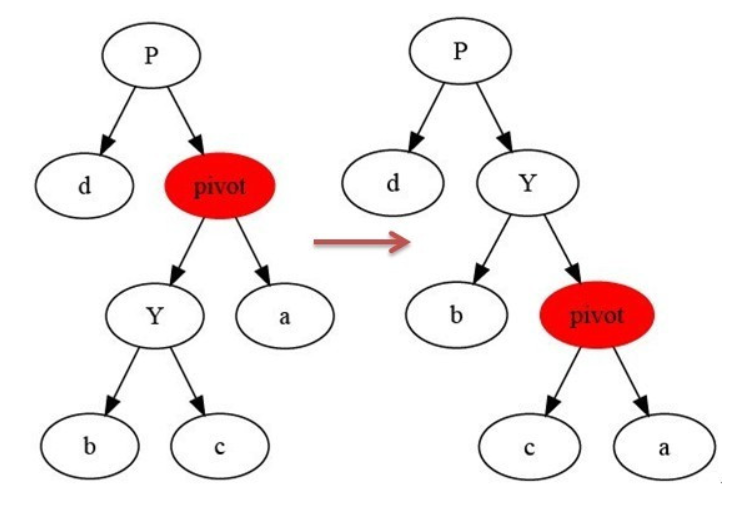
5.动图演示:
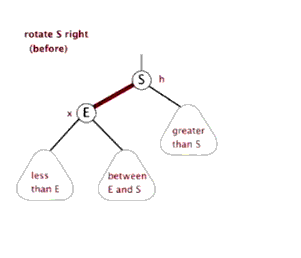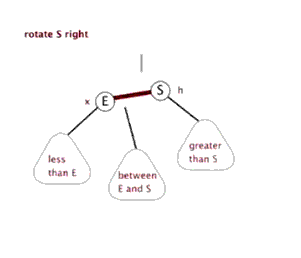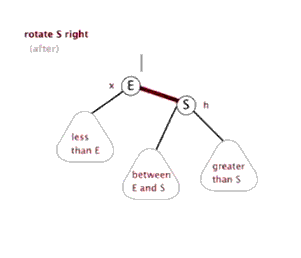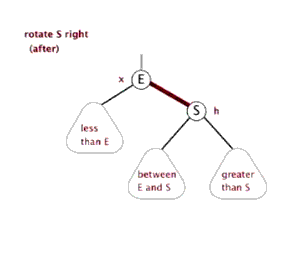
6.代码演示:
/**
* 右旋
* p为旋转的中心点
*/
public void rotateRight(Node<T,E> p) {
if (p != null) {
Node<T,E> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
为后面的红黑树等做铺垫
图片来自于网络.........





