整理 二叉树的遍历-（递归法）和（非递归法）-笔记

先序遍历、中序遍历、后续遍历、层级遍历。

1.节点信息：

package tree;
public class Node<E> {
	private E e;//数据域
	private Node<E> left;//左子树
	private Node<E> right;//右子树
	private boolean b =true;//标记是否遍历
	public Node(E e) {
		super();
		this.e = e;
	}
	public E getE() {
		return e;
	}
	public void setE(E e) {
		this.e = e;
	}
	public Node<E> getLeft() {
		return left;
	}
	public void setLeft(Node<E> left) {
		this.left = left;
	}
	public Node<E> getRight() {
		return right;
	}
	public void setRight(Node<E> right) {
		this.right = right;
	}
	public boolean getB() {
		return b;
	}
	public void setB(boolean b) {
		this.b = b;
	}
	
}

2.构造二叉树以及遍历操作：

package tree;
import java.util.Queue;
import java.util.Stack;
import java.util.concurrent.ConcurrentLinkedQueue;
/**
 * 二叉树的遍历
 * @author Administrator
 *
 */
public class Tree {
	private Node<Integer> head;
	public Tree(){
	}
	/**
	 * 添加节点
	 * @param e
	 * @return
	 */
	public boolean addNode(Integer e){
		if(head==null){//空树
			head=new Node<Integer>(e);
			return true;
		}else{//非空
			Node<Integer> n=head;
			do{
				Integer a=n.getE();
				if(e>=a){
					if(n.getRight()==null){
						Node<Integer> node=new Node<Integer>(e);
						n.setRight(node);
						return true;
					}else{
						n=n.getRight();
					}
				}else{
					if(n.getLeft()==null){
						Node<Integer> node=new Node<Integer>(e);
						n.setLeft(node);
						return true;
					}else{
						n=n.getLeft();
					}
				}
			}while(n!=null);
		}
		return false;
	}
	/**
	 * 先序遍历（递归法）
	 */
	public void preErgodic(){
		pre(head);
		System.out.println();
	}
	private void pre(Node<Integer> node){
		if(node==null){
			return;
		}
		System.out.print(node.getE()+"  ");
		pre(node.getLeft());
		pre(node.getRight());
	}
	
	/**
	 * 中序遍历（递归法）
	 */
	public void midErgodic(){
		mid(head);
		System.out.println();
	}
	private void mid(Node<Integer> node){
		if(node==null){
			return;
		}
		mid(node.getLeft());
		System.out.print(node.getE()+"  ");
		mid(node.getRight());
	}
	
	/**
	 * 后续遍历（递归法）
	 */
	public void subErgodic(){
		sub(head);
		System.out.println();
	}
	private void sub(Node<Integer> node){
		if(node==null){
			return;
		}
		sub(node.getLeft());
		sub(node.getRight());
		System.out.print(node.getE()+"  ");
	}
	
	/**
	 * 先序遍历（非递归,基于栈）
	 */
	public void _preErgodic(){
		if(head==null){
			return;
		}
		Stack<Node<Integer>> stack=new Stack<>();
		Node<Integer> node=head;
		stack.push(node);
		while(!stack.isEmpty()){
			Node<Integer> n=stack.pop();
			System.out.print(n.getE()+"  ");
			if(n.getRight()!=null){
				stack.push(n.getRight());
			}
			if(n.getLeft()!=null){
				stack.push(n.getLeft());
			}
		}
		System.out.println();
	}
	
	/**
	 * 中序遍历（非递归,基于栈）
	 */
	public void _midErgodic(){
		if(head==null){
			return;
		}
		Stack<Node<Integer>> stack=new Stack<>();
		Node<Integer> n=head;
		operation(n, stack);
		while(!stack.isEmpty()){
			n=stack.pop();
			System.out.print(n.getE()+"  ");
			if(n.getRight()!=null){
				operation(n.getRight(),stack);
			}
		}
		System.out.println();
	}
	private void operation(Node<Integer> n,Stack<Node<Integer>> s){
		s.push(n);
		while(n.getLeft()!=null){
			s.push(n.getLeft());
			n=n.getLeft();
		}
	}
	
	/**
	 * 后序遍历（非递归,基于栈）
	 */
	public void _subErgodic(){
		if(head==null){
			return;
		}
		Stack<Node<Integer>> stack=new Stack<>();
		Node<Integer> n=head;
		stack.push(n);
		boolean b=true;
		while(!stack.isEmpty()){
			n=stack.peek();
			if(n.getRight()!=null&&n.getRight().getB()){
				stack.push(n.getRight());
				b=false;
			}
			if(n.getLeft()!=null&&n.getLeft().getB()){
				stack.push(n.getLeft());
				b=false;
			}
			if(b){
				n=stack.pop();
				System.out.print(n.getE()+"  ");
				n.setB(false);
			}
			b=true;
		}
		System.out.println();
	}
	
	public void hieErgodic(){
		if(head==null){
			return;
		}
		Queue<Node<Integer>> q=new ConcurrentLinkedQueue<Node<Integer>>();
		Node<Integer> n=head;
		q.add(n);
		while(!q.isEmpty()){
			n=q.poll();
			System.out.print(n.getE()+"  ");
			if(n.getLeft()!=null){
				q.add(n.getLeft());
			}
			if(n.getRight()!=null){
				q.add(n.getRight());
			}
		}
	}
}

3.测试：

package tree;

public class TestMain {
	public static void main(String[] args) {
		Tree tree=new Tree();
		tree.addNode(10);
		tree.addNode(5);
		tree.addNode(20);
		tree.addNode(2);
		tree.addNode(4);
		tree.addNode(15);
		tree.addNode(25);
		tree.addNode(0);
		tree.addNode(1);
		tree.addNode(3);
		tree.addNode(12);
		tree.addNode(16);
		
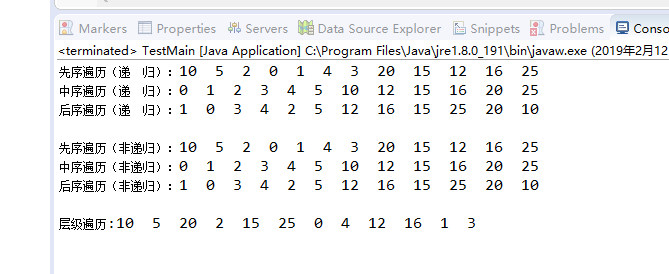
		System.out.print("先序遍历（递    归）：");
		tree.preErgodic();
		System.out.print("中序遍历（递    归）：");
		tree.midErgodic();
		System.out.print("后序遍历（递    归）：");
		tree.subErgodic();
		
		System.out.println();
		
		System.out.print("先序遍历（非递归）：");
		tree._preErgodic();
		
		System.out.print("中序遍历（非递归）：");
		tree._midErgodic();
		
		System.out.print("后序遍历（非递归）：");
		tree._subErgodic();
		
		System.out.println();
		
		System.out.print("层级遍历:");
		tree.hieErgodic();
		
	}
}