迷宫问题-寻找最短路径
迷宫问题-寻找最短路径
算法：广度优先搜索
数据结构：队列，链表
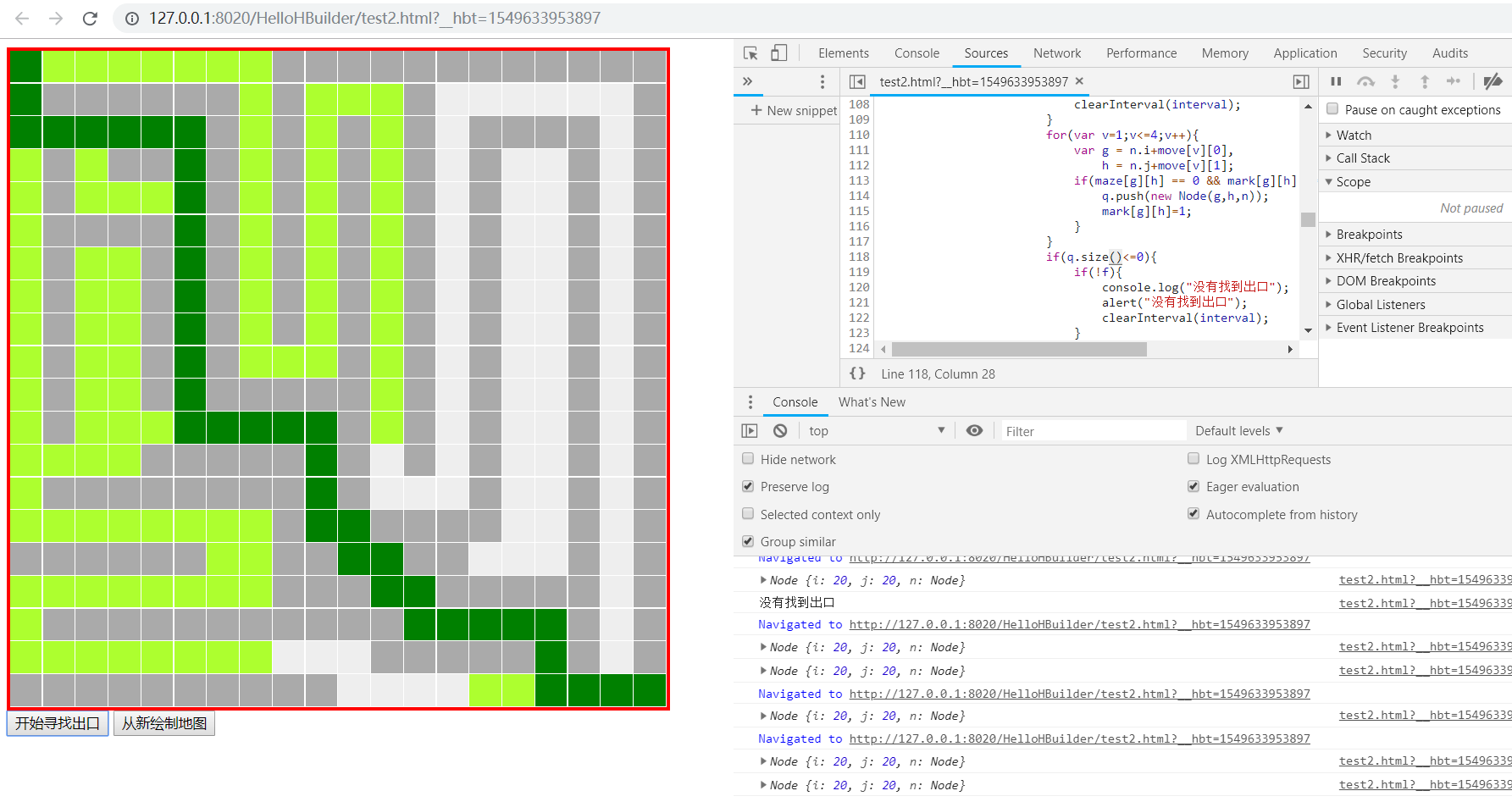
代码实现：
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title></title>
<script>
var flag=true;
window.onload = function() {
var wid=20;
var box = document.getElementById('box');
var top = 0;
for(i = 0; i < wid; i++) {//初始化地图
var left = 0;
for(j = 0; j < wid; j++) {
var odiv = document.createElement('div');
odiv.className = 'odiv';
odiv.style.top = top + 'px';
odiv.style.left = left + 'px';
odiv.setAttribute("state","1");
//odiv.innerHTML=(i+1)+"-"+(j+1);
odiv.setAttribute("id",(i+1)+"-"+(j+1));
box.appendChild(odiv);
left += 31;
}
top += 31;
}
function Node(i, j, n) { //节点信息
this.i = i;//
this.j = j;//自身节点位置坐标
this.n=n;//记录父节点
}
function ArrayQueue(){ //队列
var arr = [];
this.push = function(element){ //入队
arr.push(element);
return true;
}
this.pop = function(){ //出队
return arr.shift();
}
this.size = function(){ //队列长度
return arr.length;
}
}
var mark = new Array(); //初始化地图标记信息
function remark(){
for(var x = 0; x < (wid+2); x++) {
mark[x] = new Array(); //
for(var y = 0; y < (wid+2); y++) {
mark[x][y] = 0; //数组初始化为0
}
}
}
remark();
//方位增量
var move = [
[0, 0],
[0, 1],
[1, 0],
[0, -1],
[-1, 0]
];
var maze = [//初始化地图信息
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1],
[1,0,1,1,1,1,1,1,0,1,0,0,0,1,0,0,0,0,0,0,1,1],
[1,0,0,0,0,0,0,1,0,1,0,1,0,1,0,1,1,1,1,0,1,1],
[1,0,1,0,1,1,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,0,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,1,1,1,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,1,0,1,0,0,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,1,0,1,1,1,1,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,1,0,0,0,0,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,0,0,1,1,1,1,1,0,1,0,1,0,1,0,0,1,0,1,1],
[1,0,1,1,1,1,1,1,1,1,0,1,0,0,0,1,0,0,1,0,1,1],
[1,0,0,0,0,0,0,0,0,1,0,0,1,1,1,1,0,0,1,0,1,1],
[1,1,1,1,1,1,1,0,0,1,1,0,0,1,1,0,0,0,1,0,1,1],
[1,0,0,0,0,0,0,0,0,1,1,1,0,0,1,1,1,1,1,0,1,1],
[1,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,1,0,1,1],
[1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,1,0,1,1],
[1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]];
var interval;
var f=false;
function mazes(){
var q=new ArrayQueue();
q.push(new Node(1,1,null));
var n;
interval = window.setInterval(function() {
n=q.pop();
//console.log(n);//访问元素
document.getElementById(n.i+"-"+n.j).style.background="greenyellow";
if(n.i==wid&&n.j==wid){
console.log(n);
var p=n;
f=true;
while(p!=null){
document.getElementById(p.i+"-"+p.j).style.background="green";
p=p.n;
}
clearInterval(interval);
}
for(var v=1;v<=4;v++){
var g = n.i+move[v][0],
h = n.j+move[v][1];
if(maze[g][h] == 0 && mark[g][h] == 0){
q.push(new Node(g,h,n));
mark[g][h]=1;
}
}
if(q.size()<=0){
if(!f){
console.log("没有找到出口");
alert("没有找到出口");
clearInterval(interval);
}
}
},50);
}
//初始化地图背景
function draw(){
for(q=1;q<=20;q++){
for(w=1;w<=20;w++){
if(maze[q][w]==1){
document.getElementById(q+"-"+w).style.background="#aaa";
document.getElementById(q+"-"+w).setAttribute("state","1");
}else{
document.getElementById(q+"-"+w).style.background="#eee";
document.getElementById(q+"-"+w).setAttribute("state","0");
}
}
}
}
draw();
function begin(){
if(flag){
mazes();
flag=false;
}else{
alert("请重新绘制地图");
}
}
//从新绘制地图
function clear(){
clearInterval(interval);
remark();
draw();
flag=true;
}
//调整地图局部
function odivclick(){
var ij=this.getAttribute("id");
var arr=ij.split("-");
if(maze[parseInt(arr[0])][parseInt(arr[1])]==0){
maze[parseInt(arr[0])][parseInt(arr[1])]=1;
}else{
maze[parseInt(arr[0])][parseInt(arr[1])]=0;
}
clear();
}
document.getElementById("begin").onclick = begin;
document.getElementById("clear").onclick = clear;
//单元格添加点击事件
var list=document.getElementsByClassName('odiv');
for(var i in list) {
list[i].onclick=odivclick;
}
}
</script>
<style>
.odiv {
width: 30px;
height: 30px;
background: #aaa;
position: absolute;
font-size: 5px;
text-align: center;
line-height: 30px;
}
#box {
width: 620px;
height: 620px;
position: relative;
float: left;
border: 3px solid red;
}
#sss{
width: 1000px;
height: 500px;
float: left;
}
</style>
</head>
<body>
<div id="box">
</div>
<input type="button" value="开始寻找出口" id="begin" />
<input type="button" value="从新绘制地图" id="clear" />
</body>
</html>
猜你喜欢
weblog
8938
什么是floyd算法在计算机科学中，Floyd-Warshall算法是一种在具有正或负边缘权重（但没有负周期）的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度（加权
blog
迷宫问题-js实现
数据结构与算法
2859
迷宫问题!DOCTYPEhtmlhtml head metacharset="UTF-8" title/title script varflag=true; window.onload
blog
栈的应用-迷宫问题
数据结构与算法
7583
1.问题描述：问题：上面有一个迷宫，灰色部分代表不能通过，白色部分代表可以通过，现在从a点出发，能否找到一条路径到达b点，如果能，输出此路径。下面采用试探法求解，采用栈结构保存每一步的内容（包括坐标
blog
算法-迷宫问题-广度优先搜索-队列
数据结构与算法
8053
问题描述思路：典型的广度优先搜索算法，根据字典序大小，可以确定遍历的循序，因为字典序DLRU，所以对于每一个节点优先先往下走，然后向左走，然后向右走，然后向上走。则最后首先到达出口的一条路径就是符合
ofc
不同路径
official
93
点在下图中标记为“Start”）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？示例1输入：m=3,n=7
输出：28示例2
weblog
3041
种在图形平面上，有多个节点的路径，求出最低通过成本的算法。常用于游戏中的NPC的移动计算，或线上游戏的BOT的移动计算上。该算法像Dijkstra算法一样，可以找到一条最短路径；也像BFS一样，进行启发
blog
面试题servlet的执行过程
框架
2292
1.浏览器请求浏览器向服务器请求时，服务器不会直接执行我们的类，而是到web.xml里寻找路径名①：第一步，浏览器输入访问路径后，携带了请求行，头，体②：第二步，根据访问路径找到已注册的
ofc
二叉树的所有路径
official
155
径。说明:叶子节点是指没有子节点的节点。示例:输入:1/\23\5输出:["1-2-5","1-3"]解释:所有根节点到叶子节点的路径为:1-2-5,1-3解题思路递归得方式遍历二叉树（深度优先搜索），
最近发表
归档
2018年11月
12
2018年12月
33
2019年01月
28
2019年02月
28
2019年03月
32
2019年04月
27
2019年05月
33
2019年06月
6
2019年07月
12
2019年08月
12
2019年09月
21
2019年10月
8
2019年11月
15
2019年12月
25
2020年01月
9
2020年02月
5
2020年03月
16
2020年04月
4
2020年06月
1
2020年07月
7
2020年08月
13
2020年09月
9
2020年10月
5
2020年12月
3
2021年01月
1
2021年02月
5
2021年03月
7
标签
算法基础
linux
前端
c++
数据结构
框架
数据库
计算机基础
储备知识
java基础
ASM
其他
深入理解java虚拟机
nginx
git
消息中间件
搜索
maven
redis
docker
dubbo
目录
