最小生成树算法和其应用
什么是最小生成树:一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
对于任何一个数据结构或算法,理解和实现只是一个方面,更重要的是要明白它的应用范围或应用场景,最小生成树算法的应用非常广泛,例如:
假设要在n个城市之间建立通信联络网,则连接n个城市只需要n-1条线路。这时,自然会考虑这样一个问题,如何在节省费用的前提下建立这个通信网?自然在每两个城市之间都可以设置一条线路,而这相应的就要付出较高的经济代价。n个城市之间最多可以设置n(n-1)/2条线路,使用最小生成树算法就可以在线路中选择出一条总的代价最小的路线。
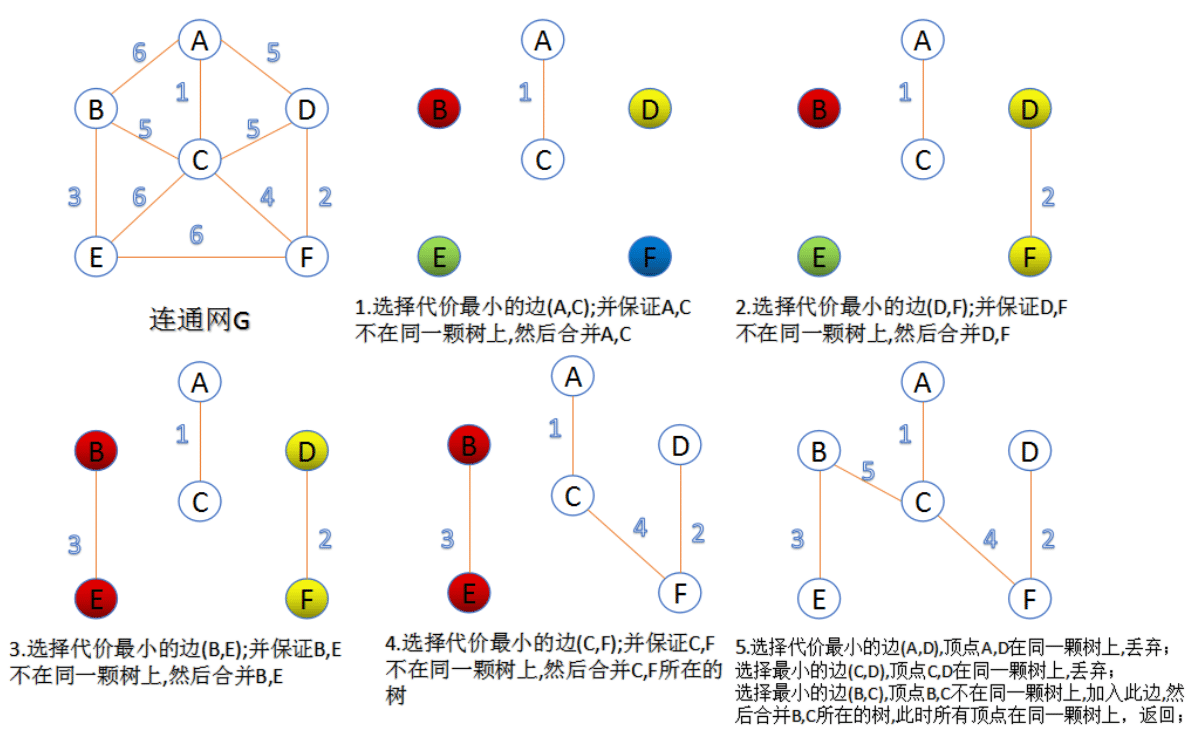
Kruskal算法的算法描述
- 把图中的所有边按代价从小到大排序;
- 把图中的n个顶点看成独立的n棵树组成的森林;
- 按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
- 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
java代码实现:
我是完全使用了面向对象的思维来设计的这个算法,原因是用面向对象的思维更方便设计。核心代码就七八行
while(lines.size()>0) {
Line l=lines.removeFirst();//从边集合中取出权值最小的一个边
if(!l.node1.tree.set.contains(l.node2)) {//边所在的两个节点是否在同一颗树上(true就是在一棵树上)
ln.add(c[l.node1.node]+"->"+c[l.node2.node]);
for(Node node:l.node1.tree.set) {//把一棵树上的节点全部移动到另外一棵树上(合并为一棵树)
node.tree=l.node2.tree;//修改节点所在的树
l.node2.tree.set.add(node);//加入树的节点集合
}
}
}
完整代码:
package 最小生成树;
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Set;
//节点
class Node{
public Node(int n) {
this.node=n;
}
public int node;//节点
public Tree tree;//节点所在的树
}
//边
class Line implements Comparable<Line>{
public Line(int cost,Node n,Node n2){
this.cost=cost;
this.node1=n;
this.node2=n2;
}
public int cost;//代价
public Node node1;
public Node node2;
@Override
public int compareTo(Line l) {//排序接口
if(this.cost>l.cost) return 1;
else if(this.cost<l.cost) return -1;
return 0;
}
@Override
public String toString() {
return cost+"";
}
}
//树
class Tree{
public Tree(Node n) {
set.add(n);
n.tree=this;
}
public Set<Node> set=new HashSet<Node>();//树的所有节点集合
}
/**
* Kruskal最小生成树算法
* @author LENOVO
*
*/
public class Kruskal {
private static char[] c= {'a','b','c','d','e','f'};
/**
* 连通图表示
*/
private static int[][] map=new int[][]{{0 ,6 ,1 ,5 ,-1,-1},
{6 ,0 ,5 ,-1,3 ,-1},
{1 ,5 ,0 ,5 ,6 ,4 },
{5 ,-1,5 ,0 ,-1,2 },
{-1,3 ,6 ,-1,0 ,6 },
{-1,-1,4 ,2 ,6 ,0 }};
public static void main(String[] args) {
Set<Tree> forest=new HashSet<Tree>();//森林
Node n[]=new Node[map.length];//所有节点集合
for(int i=0;i<map.length;i++) {//生成节点
n[i]=new Node(i);
forest.add(new Tree(n[i]));
}
LinkedList<Line> lines=new LinkedList<Line>();//所有边集合表示
for(int i=1;i<map.length;i++) {//生成边(a-b和b-a是同一个边)
for(int j=0;j<i;j++) {
if(map[i][j]>0) {
lines.add(new Line(map[i][j],n[i],n[j]));
}
}
}
Collections.sort(lines);//边集合从小到大排序
//算法开始
List<String> ln=new ArrayList<String>();
//遍历所有的边集合
while(lines.size()>0) {
Line l=lines.removeFirst();//从边集合中取出权值最小的一个边
if(!l.node1.tree.set.contains(l.node2)) {//边所在的两个节点是否在同一颗树上(true就是在一棵树上)
ln.add(c[l.node1.node]+"->"+c[l.node2.node]);
for(Node node:l.node1.tree.set) {//把一棵树上的节点全部移动到另外一棵树上(合并为一棵树)
node.tree=l.node2.tree;//修改节点所在的树
l.node2.tree.set.add(node);//加入树的节点集合
}
}
}
System.out.println(ln);//最小生成树的边的表示
}
}


